Forward-Backward Reasoning in Large Language Models for Mathematical Verification

Weisen Jiang1,2, Han Shi3, Longhui Yu4, Zhengying Liu3, Yu Zhang1s, Zhenguo Li3, James T. Kwok2,
1Southern University of Science and Technology, 2Hong Kong University of Science and Technology
3Huawei Noah’s Ark Lab, 4Peking University
Paper Code
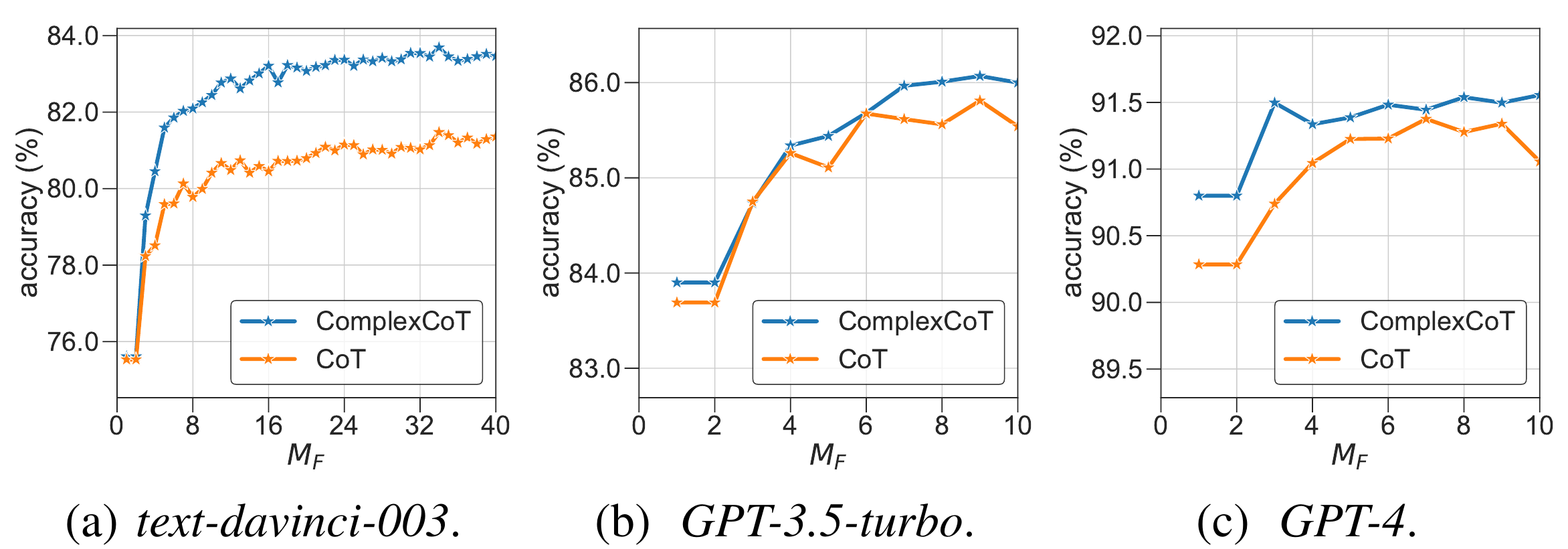
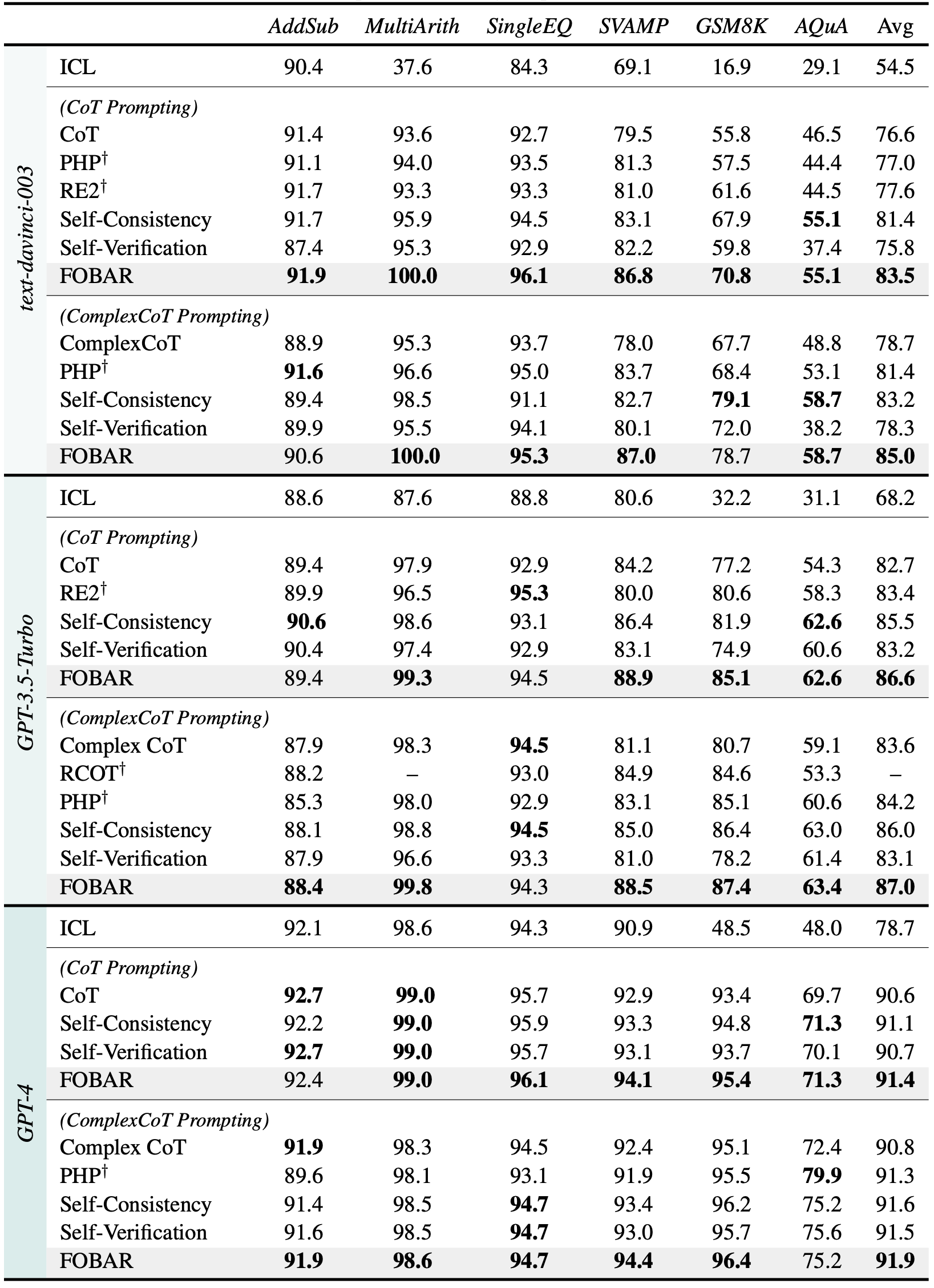
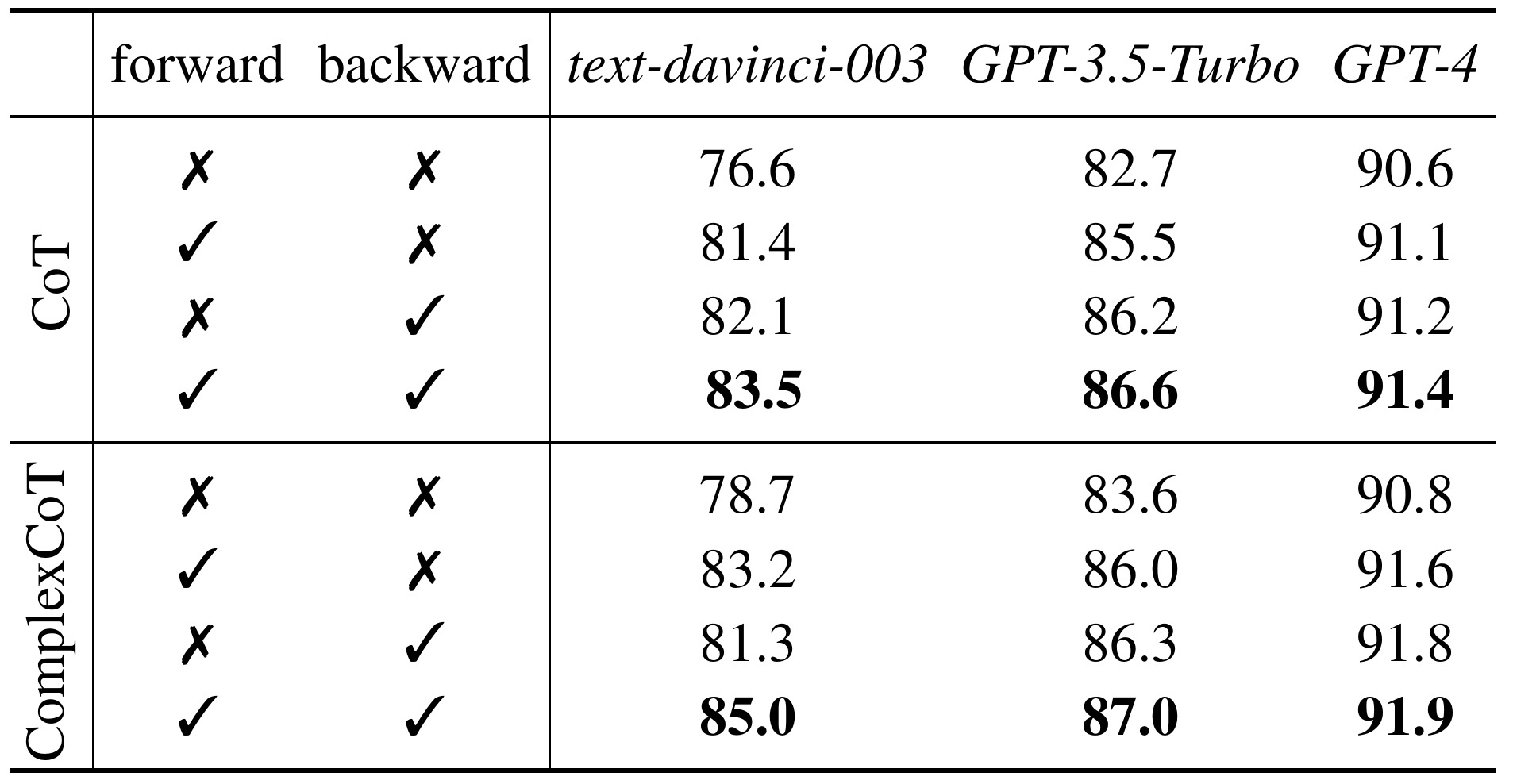
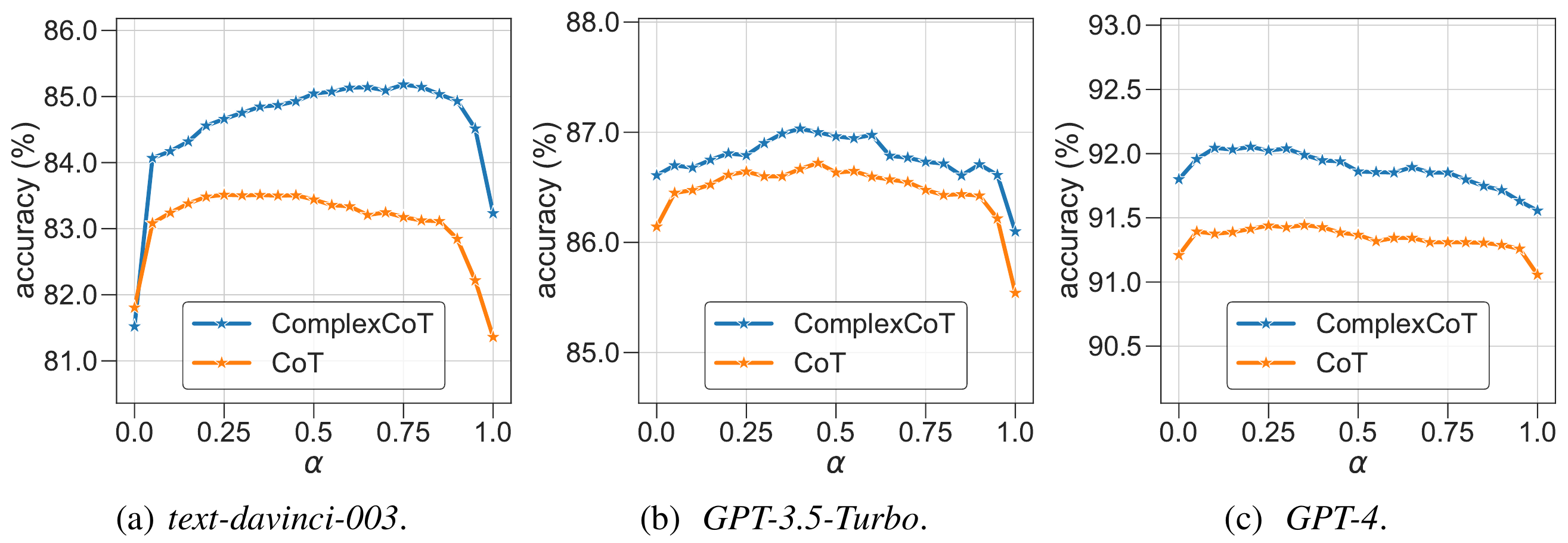
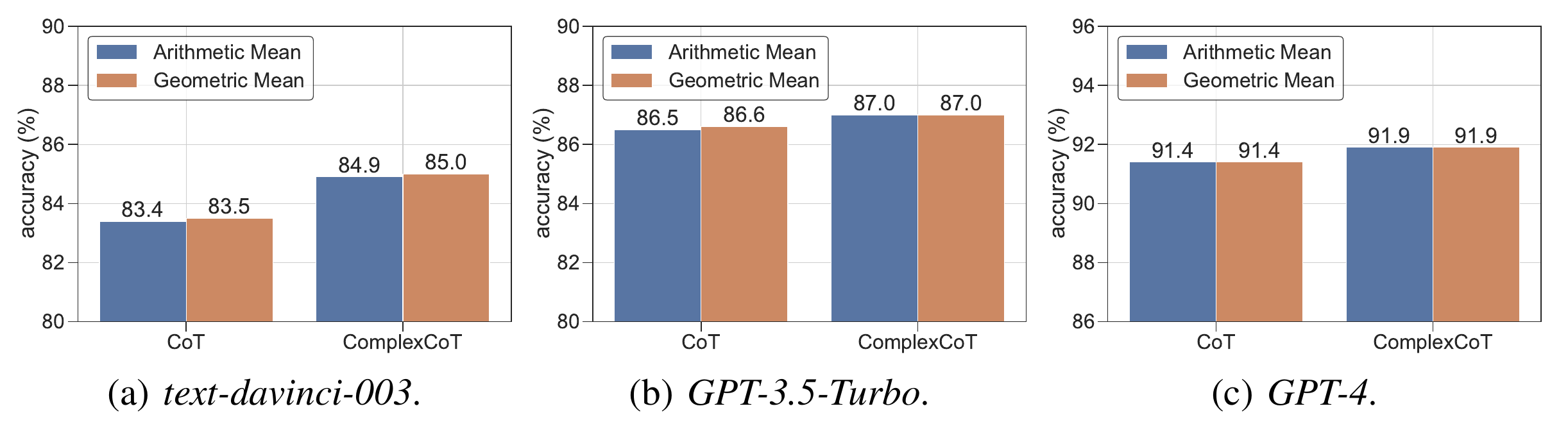
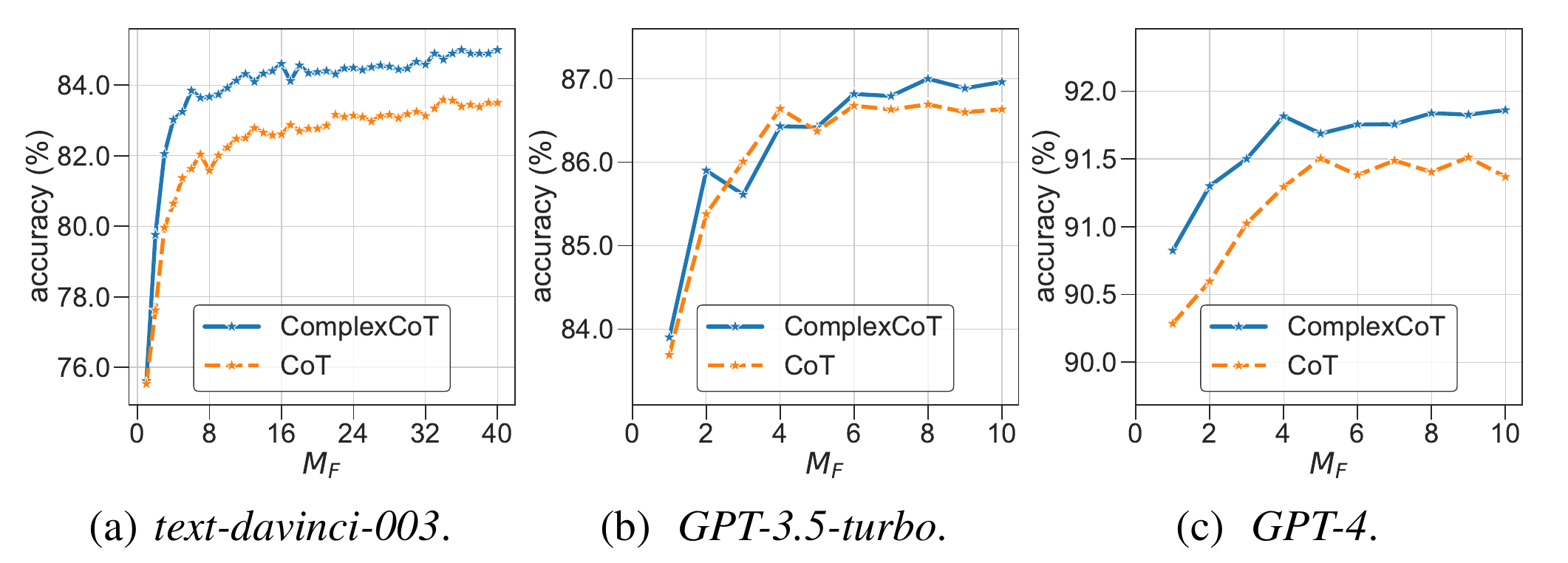
MY ALT TEXT

Abstract

Self-Consistency samples diverse reasoning chains with answers and chooses the final answer by majority voting. It is based on forward reasoning and cannot further improve performance by sampling more reasoning chains when saturated. To further boost performance, we introduce backward reasoning to verify candidate answers. Specifically, for mathematical tasks, we mask a number in the question and ask the LLM to answer a backward question created by a simple template, i.e., to predict the masked number when a candidate answer is provided. Instead of using forward or backward reasoning alone, we propose FOBAR to combine FOrward and BAckward Reasoning for verification. Extensive experiments on six standard mathematical data sets and three LLMs show that FOBAR achieves state-of-the-art performance. In particular, FOBAR outperforms Self-Consistency, which uses forward reasoning alone, demonstrating that combining forward and backward reasoning is more accurate in verification. In addition, FOBAR achieves higher accuracy than existing verification methods, showing the effectiveness of the simple template used in backward reasoning and the proposed combination.

Contributions

Introduce Backward Reasoning to Mathematical Verification

  1. A simple template is proposed to create backward questions: We mask a number in the question, and append the template with a candidate answer
  2. We design a CoT prompt for the LLM to predict the masked number
  3. We estimate the probability of the candidate answer based on the number of correct chains in the backward direction

Propose FOBAR to Combine Forward and Backward Reasoning for Verifying Candidate Answers

  1. Combine forward and backward probabilities of candidate answers in a soft manner $$\mathbb{P} (\hat{A}_c) \propto (\mathbb{P} (\hat{A}_c; \text{forward}))^{\alpha} (\mathbb{P} (\hat{A}_c; \text{backward}))^{1-\alpha} $$
  2. When $\alpha=1$, it recovers the SOTA Self-Consistency
  3. When $\alpha=0$, it recovers the Backward Reasoning for Verification
  4. The combination is flexible, other methods like arithmetic mean can be used

Extensive Experiments on Various Mathematical Data Sets

  1. FOBAR achieves SOTA performance
  2. FOBAR outperforms Self-Consistency, demonstrating that combining forward and backward reasoning together is better
  3. FOBAR achieves higher accuracy than Self-Verification, confirming that using the simple template in backward reasoning and the proposed combination is more effective

Performance of Self-Consistency Saturates Quickly When Increasing #Paths $M_F$

MY ALT TEXT

Template for Generating Questions in Backward Reasoning

Question

Jim spends 2 hours watching TV and then decides to go to bed and reads for half as long. He does this 3 times a week. How many hours does he spend on TV and reading in 4 weeks? (ground-truth answer: 36)
(candidate answers: 36, 12)

Template

If we know the answer to the above question is $\hat{A}_c$, what is the value of unknown variable ${\bf x}$?

Questions for Backward Reasoning (candidate answer: 36)

Jim spends ${\bf x}$ hours watching TV and then decides to go to bed and reads for half as long. He does this 3 times a week. How many hours does he spend on TV and reading in 4 weeks? If we know the answer to the above question is 36, what is the value of unknown variable ${\bf x}$?

Jim spends 2 hours watching TV and then decides to go to bed and reads for half as long. He does this ${\bf x}$ times a week. How many hours does he spend on TV and reading in 4 weeks? If we know the answer to the above question is 36, what is the value of unknown variable ${\bf x}$?

Jim spends 2 hours watching TV and then decides to go to bed and reads for half as long. He does this 3 times a week. How many hours does he spend on TV and reading in ${\bf x}$ weeks? If we know the answer to the above question is 36, what is the value of unknown variable ${\bf x}$?

Questions for Backward Reasoning (candidate answer: 12)

Jim spends ${\bf x}$ hours watching TV and then decides to go to bed and reads for half as long. He does this 3 times a week. How many hours does he spend on TV and reading in 4 weeks? If we know the answer to the above question is 12, what is the value of unknown variable ${\bf x}$?

Jim spends 2 hours watching TV and then decides to go to bed and reads for half as long. He does this ${\bf x}$ times a week. How many hours does he spend on TV and reading in 4 weeks? If we know the answer to the above question is 12, what is the value of unknown variable ${\bf x}$?

Jim spends 2 hours watching TV and then decides to go to bed and reads for half as long. He does this 3 times a week. How many hours does he spend on TV and reading in ${\bf x}$ weeks? If we know the answer to the above question is 12, what is the value of unknown variable ${\bf x}$?

Experiments

Main Results

MY ALT TEXT

Usefulness of Forward and Backward Reasoning

MY ALT TEXT

Ablation Study

BibTeX


@InProceedings{jiang2024fobar,
  title={Forward-Backward Reasoning in Large Language Models for Mathematical Verification},
  author={Jiang, Weisen and Shi, Han and Yu, Longhui and Liu, Zhengying and Zhang, Yu and Li, Zhenguo and Kwok, James T},
  booktitle={Findings of Annual Meeting of the Association for Computational Linguistics},
  year={2024}
}